Y Wing / XY Wing
XY Wing (sometimes called Y Wing) is another advanced technique for eliminating candidates.
It starts by finding a cell with only two candidates (a bi-value cell) called the pivot.
These 2 candidates are called X and Y.
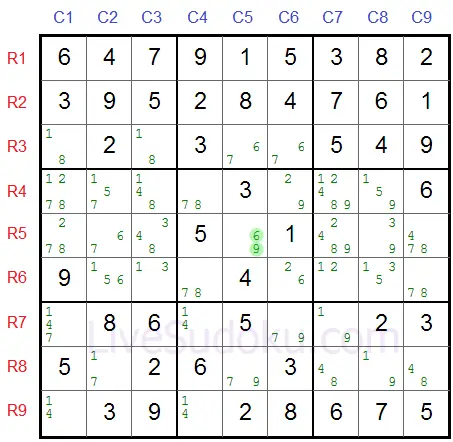
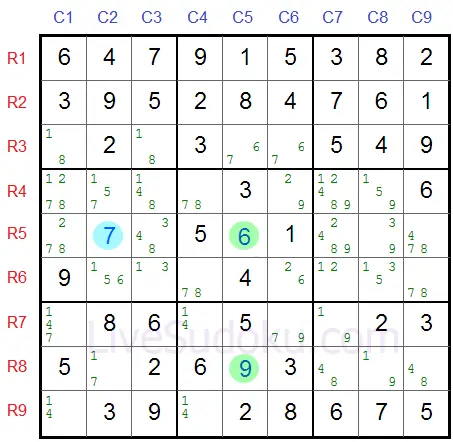
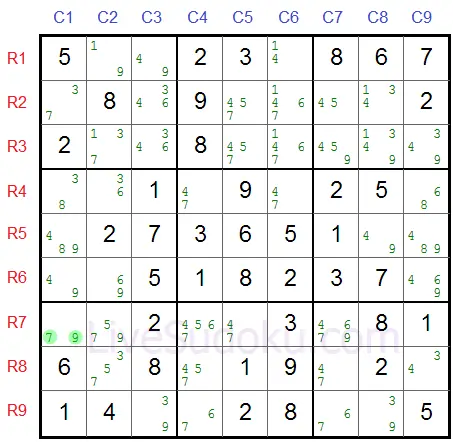
In our sample - R5C5 is the pivot, X=6 and Y=9.
Next, we look for two more bi-valued cells that are buddy cells with the pivot.
They are called pincers, one should have X and Z as candidates and the other one - Y and Z.
Z is any digit different than X and Y.
In our example Z=7 and the pincers are R5C2 (same row as pivot) and R8C5 (same column).
R5C2 candidates are 6 and 7 (X=6, Z=7).
R8C5 candidates are 9 and 7 (Y=9, Z=7).
In XY Wing we are interested in Z and the other cells it's affecting.
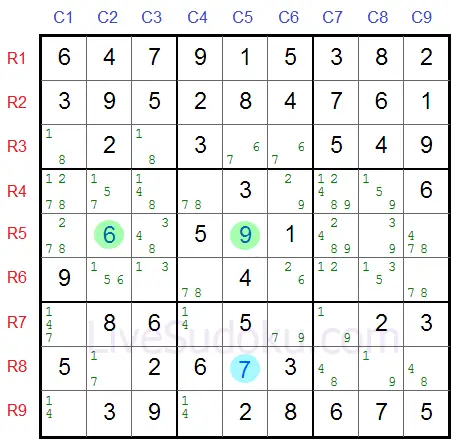
There are only two options for the pivot (6 or 9) and it's pincers to resolve:
if pivot=6 (X) then:
R8C5=9 (Y) and R5C2=7 (Z).
or the second option, if pivot=9 (Y) then:
R8C5=6 (X) and R5C2=7 (Z).
Either way, one of the pincers R5C2 or R8C5 has to be a 7 (Z) marked in blue:
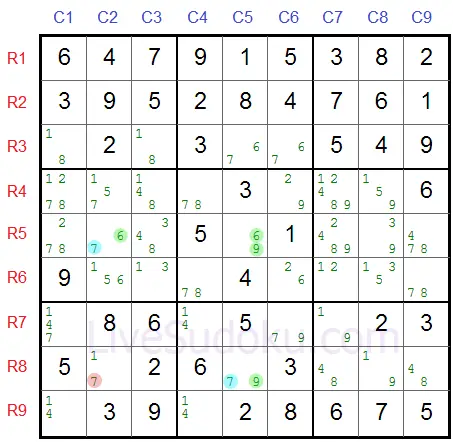
Therefore, any cell that is a buddy with both pincers R5C2 or R8C5 cannot be a 7 (Z).
Take R8C2 - we can definitely remove 7 (Z) from its candidate list:
The previous example had a shape of an X but it isn't necessarily has to be so.
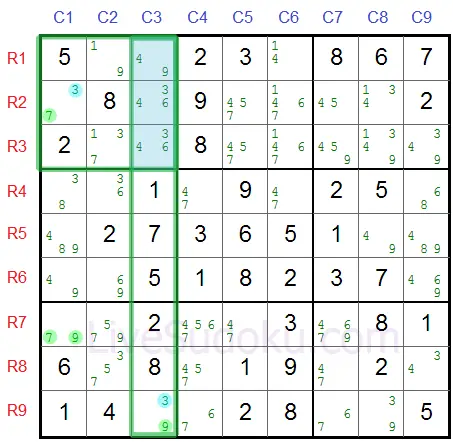
Let's have a look at another example where R7C1 is the pivot:
R2C1 is one pincer (it's on the same column as the pivot).
R9C3 is the second pincer (it's in the same box as the pivot).
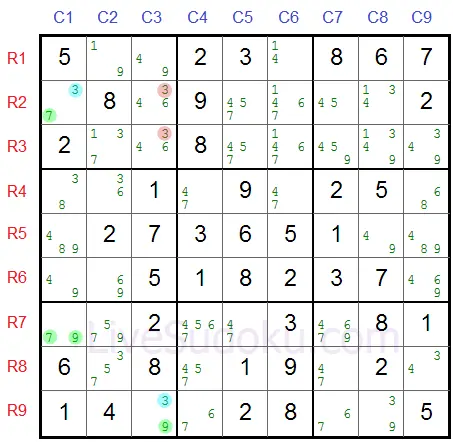
X=7, Y=9 and Z=3 (marled in blue)
Any cell that is buddy with both pincers R2C1 and R9C3 cannot be 3 (Z).
If we can find such cells that have 3 as a candidate we can remove 3 from their candidates.
The buddy cells of both pincers are marked in blue.
Can you find which cells cannot be a 3?
The answer is both R2C3 and R3C3.
They are in the same box as the first pincer - R2C1 and in the same column as the second pincer R9C3.
They cannot be a 3 so we can remove it from their candidates list.
This time we eliminated Z from two cells, XY is not limited for affecting only one cells but all cells that fits its rules.
How to find them
XY wings must involve 3 buddy cells that are bi-value (have only 2 candidates each) so start by searching for 3 bi-value buddy such.
Those 3 cells must then have XY, XZ and YZ as candidates.
One you find this scenario, look for the buddy cells of both XZ and YZ cells and eliminate Z from those.